library(lubridate)
library(ggplot2)
library(car)
#library(forecast)
library(lmtest)Loading required package: zoo
Attaching package: ‘zoo’
The following objects are masked from ‘package:base’:
as.Date, as.Date.numeric
김보람
October 10, 2023
해당 자료는 전북대학교 이영미 교수님 2023고급시계열분석 자료임
다음은 어느 서점에서 최근 10 일동안 판매된 경제 서적의 일별 판매액 (단위 : 만원)을 나타내는 시계열 자료이다. 이 자료에 상수평균모형을 적합시키려 한다.
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(Z_t\) | 52 | 46 | 46 | 52 | 50 | 50 | 48 | 45 | 41 | 53 |
상수평균모형을 적합하여라.
상수평균모형 \(Z_t = \beta_0 + \epsilon_t\)
LSE: \(\hat {\beta_0} = \bar{Z}=48.3\)
\(\hat{Z_t} = \hat{\beta_0} = 48.3\)
미래값 \(Z_{10+l}\) 에 대한 예측값 \(\hat{Z}_{10}(l)\)을 구하시오. \((l = 1, 2, 3, 4, 5)\)
note 시점 n에서의 l-시차 후의 예측값: \(\hat{Z_n(l)} = \hat{\beta_0} = \bar{Z}\)
\(\hat{Z}_{10}(1)=\hat{Z}_{10}(2)=\hat{Z}_{10}(3)=\hat{Z}_{10}(4)=\hat{Z}_{10}(5)=48.3\)
미래값 \(Z_{10+l}, l = 1, 2, 3, 4, 5\)에 대한 95% 예측구간을 구하고, 예측값 및 예측구간의 하한값과 상한값을 관측값 \(Z_t\)의 시계열과 함께 표시하여라.
note \(Z_{n+l}\)의 \(100(1-\alpha)\)% 예측 구간: \(\bar{Z} \pm t_{\alpha/2}(n-1) \times \sqrt{(1+\frac{1}{n})s^2}\)
다음은 신장개업한 어느 편의점의 15 주간 주별 매출액을 나타낸 시계열자료이다. 이 자료에 선형추세모형을 적합시키려 한다.
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(Z_t\) | 303 | 298 | 303 | 314 | 303 | 314 | 310 | 324 | 317 | 327 | 323 | 324 | 331 | 330 | 332 |
선형추세모형을 쓰시오.
Call:
lm(formula = z ~ t, data = df)
Residuals:
Min 1Q Median 3Q Max
-6.710 -2.331 -1.181 2.519 7.133
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 297.781 2.364 125.964 < 2e-16 ***
t 2.386 0.260 9.176 4.84e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.351 on 13 degrees of freedom
Multiple R-squared: 0.8662, Adjusted R-squared: 0.856
F-statistic: 84.19 on 1 and 13 DF, p-value: 4.836e-07note \(Z_t=\beta_0+\beta_1 t + \epsilon_t, \epsilon_t \sim N(0,\sigma^2), i.i.d\)
최소제곱법에 의하여 구한 \(β_0, β_1\)의 추정량이 각각 다음과 같아짐을 보여라.
\[\hat{\beta_0} = \frac{2(2n+1)}{n(n-1)} \sum_{t=1}^n Z_t - \frac{6}{n(n-1)} \sum_{t=1}^n t_t\]
\[\hat{\beta_1} = \frac{12}{n(n^2-1)} \sum_{t=1}^n t Z_t - \frac{6}{n(n-1)} \sum_{t=1}^n Z_t\]
\(Z_t = \beta_0 + \beta_1 t + \epsilon_t\)
최소제곱법을 통해 \(\beta\)값 추정하자.
\(S = \sum_{t=1}^n \epsilon_t^2 = \sum_{t=1}^n(Z_t-\beta_0-\beta_1t)^2\)
\(\dfrac{\delta S}{\delta \beta_0}=\sum_{t=1}^n (Z_t-\beta_0 -\beta_1t)(-1)=0\) - (a)라고 하자
\(\dfrac{\delta S}{\delta \beta_1}=\sum_{t=1}^n (Z_t-\beta_0 -\beta_1t)(-t)=0\) -(b)라고 하자.
(a)식을 \(\beta_0\)에 관하여 풀면
\(\sum_{t=1}^n Z_t - n \hat{\beta}_0 - \hat{\beta}_1 \sum_{t=1}^n t = 0\)
\(\hat{\beta}_0 = \dfrac{\sum_{t=1}^n Z_t -\hat{\beta}_1 \sum_{t=1}^n t }{n}= \dfrac{\sum_{t=1}^n Z_t}{n} - \hat{\beta}_1 \dfrac{(n+1)}{2}\) -(c)라고 하자
(b)식을 정리하면,
\(\sum_{t=1}^n t Z_t = \hat{\beta}_0 \sum_{t=1}^n t + \hat{\beta}_1 \sum_{t=1}^n t^2=\hat{\beta}_0 \dfrac{n(n+1)}{2} + \hat{\beta}_1 \dfrac{n(n+1)(2n+1)}{6}\)
(c)식을 (b)식에 대입 후 연립방정식을 풀자
\(=\left( \dfrac{\sum_{t=1}^n Z_t}{n} - \hat{\beta}_1 \dfrac{(n+1)}{2} \right) \dfrac{n(n+1)}{2} + \hat{\beta}_1 \dfrac{n(n+1)(2n+1)}{6}\)
\(=\dfrac{(n+1)}{2} \sum_{t=1}^n Z_t + \hat{\beta}_1 \left( \dfrac{2n(n+1)(2n+1) -3n(n+1)^2}{12} \right)\)
\(=\dfrac{(n+1)}{2} \sum_{t=1}^n Z_t + \hat{\beta}_1 \left( \dfrac{n(n+1)(n-1)}{12} \right)\)
즉 \(\sum_{t=1}^n t Z_t =\dfrac{(n+1)}{2} \sum_{t=1}^n Z_t + \hat{\beta}_1 \left( \dfrac{n(n+1)(n-1)}{12} \right)\)
\(\hat{\beta}_1 \left( \dfrac{n(n+1)(n-1)}{12} \right) = \sum_{t=1}^n t Z_t - \dfrac{(n+1)}{2} \sum_{t=1}^n Z_t\)
\(\hat{\beta_1} = \frac{12}{n(n^2-1)} \sum_{t=1}^n t Z_t - \frac{6}{n(n-1)} \sum_{t=1}^n Z_t\)
\(\hat{\beta}_1\) 값 (c)식에 대입
\(\hat{\beta}_0 = \dfrac{\sum_{t=1}^n Z_t}{n} - \hat{\beta}_1 \dfrac{(n+1)}{2}\)
\(=\dfrac{\sum_{t=1}^n Z_t}{n} - \dfrac{6}{n(n-1)} \sum_{t=1}^n tZ_t + \dfrac{3(n+1)}{n(n-1)} \sum_{t=1}^n Z_t\)
\(=\dfrac{2(2n+1)}{n(n-1)} \sum_{t=1}^n Z_t - \dfrac{6}{n(n-1)} \sum_{t=1}^n t_t Z_t\)
선형추세모형을 적합하시오. (회귀계수 추정 및 모형 결과 설명)
\(\hat{Z}_t=\hat{\beta_0}+\hat{\beta_1}t = 297.7714 + 2.3786 t\)
위 (2)식에 대입하기
t가 1씩 증가할수록 해당 편의점의 매출액은 2.38만큼 증가한다.
미래값 \(Z_{15+l}\) 에 대한 예측값 \(\hat {Z}_{15}(l)\)을 구하시오. \((l = 1, 2, 3, 4, 5)\)
- 손게산 하는 방법
\(\hat{Z}_{n}(l) = \hat{\beta}_0 + \hat{\beta}_1(n+l)\)
- 코드
| t | y |
|---|---|
| <int> | <fct> |
| 16 | 1 |
| 17 | 2 |
| 18 | 3 |
| 19 | 4 |
| 20 | 5 |
Call:
lm(formula = z ~ t, data = data)
Residuals:
Min 1Q Median 3Q Max
-6.710 -2.331 -1.181 2.519 7.133
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 297.781 2.364 125.964 < 2e-16 ***
t 2.386 0.260 9.176 4.84e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.351 on 13 degrees of freedom
Multiple R-squared: 0.8662, Adjusted R-squared: 0.856
F-statistic: 84.19 on 1 and 13 DF, p-value: 4.836e-07(R 실습) 다음과 같은 시계열모형으로부터 모의시계열자료 \(\{Z_t, t = 1, 2, . . . , 100 \}\)을 생성한 후 4개의 시계열그림을 겹쳐 그려보고 비교하여라. 그리고 각 모의시계열자료의 표본평균과 표본분 산을 구하고, 이론적인 평균 및 분산과 비료하여라.
\(Z_t = 100 + ϵ_t\), 단 \(ϵ_t\)는 서로 독립이고 \(N(0, 1)\) 분포를 따른다.
\(E(Z_t)=E(100+\epsilon_t) = 100 + E(\epsilon_t) = 100 + 0 = 100\)
\(Var(Z_t) = Var(100+\epsilon_t) = Var(\epsilon_t) = 1 = 1\)
\(Z_t = 500 + ϵ_t\), 단 \(ϵ_t\)는 서로 독립이고 \(N(0, 1)\) 분포를 따른다.
\(E(Z_t)=E(500+\epsilon_t) = 500 + E(\epsilon_t) = 500 + 0 = 500\)
\(Var(Z_t) = Var(500+\epsilon_t) = Var(\epsilon_t) = 1 = 1\)
\(Z_t = 100 + ϵ_t\), 단 \(ϵ_t\)는 서로 독립이고 \(N(0, 100)\) 분포를 따른다.
\(E(Z_t)=E(100+\epsilon_t) = 100 + E(\epsilon_t) = 100 + 0 = 100\)
\(Var(Z_t) = Var(100+\epsilon_t) = Var(\epsilon_t) = 100 = 100\)
\(Z_t = 100 + tϵ_t\), 단 \(ϵ_t\)는 서로 독립이고 \(N(0, 1)\) 분포를 따른다.
\(E(Z_t)=E(100+ t \epsilon_t) = 100 + t E(\epsilon_t) = 100 + t 0 = 100\)
\(Var(Z_t) = Var(100+ t \epsilon_t) = Var(t \epsilon_t) = t^2 Var(\epsilon_t) = t^2 \times 1 = t^2\)
- ggplot
ggplot(data=df, aes(t)) +
geom_line(aes(y=z1, colour='z1')) +
geom_line(aes(y=z2, colour='z2')) +
geom_line(aes(y=z3, colour='z3')) +
geom_line(aes(y=z4, colour='z4')) +
ylab('z')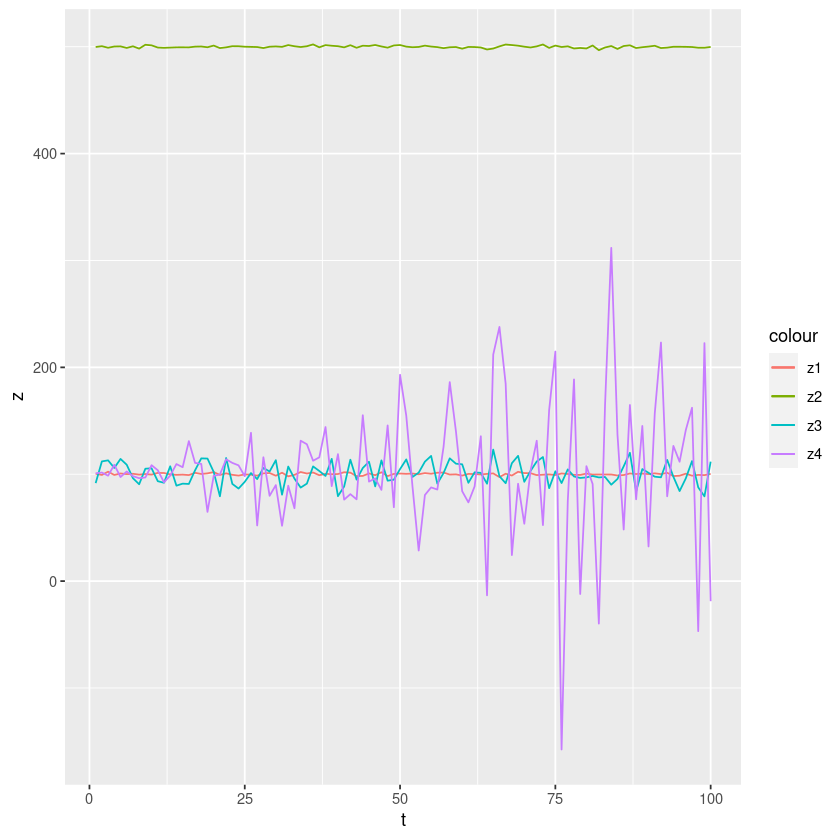
- plot
(R 실습) 다음과 같은 시계열모형으로부터 모의시계열자료 \(\{Z_t, t = 1, 2, . . . , 100 \}\)을 생성한 후 \(Z_t\)와 \(E(Z_t)\)의 시계열그림을 겹쳐 그려라. 또한 이 시계열 자료들은 각각 어떤 성분으로 구성되어 있는지 설명하여라. 단 오차항 \(ϵ_t\)는 서로 독립인 \(N(0, 1)\) 분포를 가정한다.
\(Z_t = 100 + ϵ_t\)
상수평균모형: 불규칙성분만을 갖는 경우
\(Z_t = 100 + t + ϵ_t\)
선형추세모형: 직선형인 추세를 가지고 증가
\(Z_t = 100 + 0.3t + sin \left( \frac{2πt}{12} \right)+ cos \left(\frac{2πt}{12} \right) + ϵ_t\)
선형계절추세모형: 추세 및 계절 성분을 가진다..
(R 실습) “book.txt”는 한 서점에서 첫 30일동안 팔린 어느 베스트셀러의 일별 판매 부수(단위 : 권) 시계열자료이다.
시계열 그림을 그리시오.
이 시계열 자료는 어떤 성분으로 구성되어 있는지 설명하시오.
선형 추세 모형
적절한 추세모형을 적합하여라.
Call:
lm(formula = book ~ t, data = data)
Residuals:
Min 1Q Median 3Q Max
-2.5563 -1.0063 -0.2081 1.0385 2.0644
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.19080 0.46960 17.44 <2e-16 ***
t 3.07586 0.02645 116.28 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.254 on 28 degrees of freedom
Multiple R-squared: 0.9979, Adjusted R-squared: 0.9979
F-statistic: 1.352e+04 on 1 and 28 DF, p-value: < 2.2e-16\(\hat{Z}_t = 8.19080 + 3.07586 t\)
마지막 관측값으로 부터 \(Z_{n+l}\) 에 대한 예측값 \(\hat{Z}_n (l)\)을 구하시오. \((n = 30, l = 1, 2, . . . , 12)\)
| t | y |
|---|---|
| <int> | <fct> |
| 31 | 1 |
| 32 | 2 |
| 33 | 3 |
| 34 | 4 |
| 35 | 5 |
| 36 | 6 |
| 37 | 7 |
| 38 | 8 |
| 39 | 9 |
| 40 | 10 |
| 41 | 11 |
| 42 | 12 |
마지막 관측값으로 부터 \(Z_{n+l}(n = 30, l = 1, 2, . . . , 12)\)에 대한 95% 예측구간을 구하여라
predict_result <- as.data.frame(predict(m, newdata = new_data, interval = "predict",level=0.95))
predict_result| fit | lwr | upr | |
|---|---|---|---|
| <dbl> | <dbl> | <dbl> | |
| 1 | 103.5425 | 100.7996 | 106.2855 |
| 2 | 106.6184 | 103.8584 | 109.3784 |
| 3 | 109.6943 | 106.9162 | 112.4723 |
| 4 | 112.7701 | 109.9731 | 115.5671 |
| 5 | 115.8460 | 113.0291 | 118.6629 |
| 6 | 118.9218 | 116.0842 | 121.7595 |
| 7 | 121.9977 | 119.1384 | 124.8570 |
| 8 | 125.0736 | 122.1918 | 127.9554 |
| 9 | 128.1494 | 125.2443 | 131.0546 |
| 10 | 131.2253 | 128.2960 | 134.1546 |
| 11 | 134.3011 | 131.3469 | 137.2554 |
| 12 | 137.3770 | 134.3970 | 140.3570 |
예측값 및 예측구간의 하한값과 상한값을 관측값 \(Z_t\)의 시계열과 함께 표시하여라.
(R 실습) “export.txt”는 월별수출액(단위:억$) 시계열자료이다.
시계열 그림을 그리시오.
이 시계열 자료는 어떤 성분으로 구성되어 있는지 설명하시오.
선형 계절 추세 모형
적절한 추세모형을 적합하여라. (지시함수 사용)
이분산성이 있어보이니 로그변환 실시
| day | export | lnex | y | trend | |
|---|---|---|---|---|---|
| <date> | <dbl> | <dbl> | <fct> | <int> | |
| 1 | 1984-01-01 | 20.40 | 3.015535 | 1 | 1 |
| 2 | 1984-02-01 | 23.01 | 3.135929 | 2 | 2 |
| 3 | 1984-03-01 | 25.73 | 3.247658 | 3 | 3 |
| 4 | 1984-04-01 | 25.55 | 3.240637 | 4 | 4 |
| 5 | 1984-05-01 | 29.96 | 3.399863 | 5 | 5 |
| 6 | 1984-06-01 | 31.94 | 3.463859 | 6 | 6 |
Call:
lm(formula = lnex ~ trend + y, data = tmp.data)
Residuals:
Min 1Q Median 3Q Max
-0.242037 -0.076076 -0.000101 0.061002 0.228615
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.2478546 0.0465045 69.840 < 2e-16 ***
trend 0.0097170 0.0005074 19.151 < 2e-16 ***
y2 0.0449215 0.0580829 0.773 0.441781
y3 0.2113353 0.0601535 3.513 0.000764 ***
y4 0.1732163 0.0601385 2.880 0.005212 **
y5 0.2230338 0.0601278 3.709 0.000402 ***
y6 0.2902377 0.0601214 4.828 7.39e-06 ***
y7 0.2196982 0.0601192 3.654 0.000483 ***
y8 0.1847631 0.0601214 3.073 0.002977 **
y9 0.2563299 0.0601278 4.263 5.95e-05 ***
y10 0.2416985 0.0601385 4.019 0.000141 ***
y11 0.2741932 0.0601535 4.558 2.03e-05 ***
y12 0.3781424 0.0601727 6.284 2.14e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1162 on 73 degrees of freedom
Multiple R-squared: 0.8596, Adjusted R-squared: 0.8365
F-statistic: 37.25 on 12 and 73 DF, p-value: < 2.2e-16- 제약조건 \(\beta_1=0\)
s2는 1월보다 0.0449215만큼 더 팔리고
s3는 1월보다 0.0449215만큼 더 팔린다.
s2는 유의하지 않게 나왔는데 이는 1월과 2월의 시간차이가 적기 때문이다.
Call:
lm(formula = lnex ~ 0 + trend + y, data = tmp.data)
Residuals:
Min 1Q Median 3Q Max
-0.242037 -0.076076 -0.000101 0.061002 0.228615
Coefficients:
Estimate Std. Error t value Pr(>|t|)
trend 0.0097170 0.0005074 19.15 <2e-16 ***
y1 3.2478546 0.0465045 69.84 <2e-16 ***
y2 3.2927761 0.0467447 70.44 <2e-16 ***
y3 3.4591898 0.0481580 71.83 <2e-16 ***
y4 3.4210709 0.0483687 70.73 <2e-16 ***
y5 3.4708884 0.0485837 71.44 <2e-16 ***
y6 3.5380923 0.0488031 72.50 <2e-16 ***
y7 3.4675528 0.0490268 70.73 <2e-16 ***
y8 3.4326177 0.0492547 69.69 <2e-16 ***
y9 3.5041845 0.0494867 70.81 <2e-16 ***
y10 3.4895531 0.0497228 70.18 <2e-16 ***
y11 3.5220478 0.0499630 70.49 <2e-16 ***
y12 3.6259970 0.0502071 72.22 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1162 on 73 degrees of freedom
Multiple R-squared: 0.9992, Adjusted R-squared: 0.9991
F-statistic: 7394 on 13 and 73 DF, p-value: < 2.2e-16
Call:
lm(formula = lnex ~ trend + y, data = tmp.data, contrasts = list(y = "contr.sum"))
Residuals:
Min 1Q Median 3Q Max
-0.242037 -0.076076 -0.000101 0.061002 0.228615
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.4559854 0.0253853 136.141 < 2e-16 ***
trend 0.0097170 0.0005074 19.151 < 2e-16 ***
y1 -0.2081308 0.0395338 -5.265 1.36e-06 ***
y2 -0.1632093 0.0395338 -4.128 9.59e-05 ***
y3 0.0032044 0.0420579 0.076 0.9395
y4 -0.0349145 0.0420334 -0.831 0.4089
y5 0.0149030 0.0420150 0.355 0.7238
y6 0.0821069 0.0420028 1.955 0.0544 .
y7 0.0115674 0.0419967 0.275 0.7838
y8 -0.0233678 0.0419967 -0.556 0.5796
y9 0.0481991 0.0420028 1.148 0.2549
y10 0.0335677 0.0420150 0.799 0.4269
y11 0.0660624 0.0420334 1.572 0.1204
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1162 on 73 degrees of freedom
Multiple R-squared: 0.8596, Adjusted R-squared: 0.8365
F-statistic: 37.25 on 12 and 73 DF, p-value: < 2.2e-16적합 결과를 설명하여라. (회귀계수의 의미 설명)
모형의 p-value값은 \(<2.2e^{-16}\)이므로 모형은 유의하고 \(R^2\)값도 85퍼의 설명력을 가진다. 각 회귀계수도 유의미하며, ..
| hat_y1 | hat_y2 | hat_y3 | |
|---|---|---|---|
| <dbl> | <dbl> | <dbl> | |
| 1 | 3.257572 | 3.257572 | 3.257572 |
| 2 | 3.312210 | 3.312210 | 3.312210 |
| 3 | 3.488341 | 3.488341 | 3.488341 |
| 4 | 3.459939 | 3.459939 | 3.459939 |
| 5 | 3.519473 | 3.519473 | 3.519473 |
| 6 | 3.596394 | 3.596394 | 3.596394 |
마지막 관측값으로 부터 \(Z_{n+l}\) 에 대한 예측값 \(\hat{Z}_n(l)\)을 구하시오. \((n = 30, l = 1, 2, . . . , 12)\)
문제 오류인듯? n=86이여야 하는 것 같다.
| day | export | lnex | y | trend | |
|---|---|---|---|---|---|
| <date> | <dbl> | <dbl> | <fct> | <int> | |
| 1 | 1984-01-01 | 20.40 | 3.015535 | 1 | 1 |
| 2 | 1984-02-01 | 23.01 | 3.135929 | 2 | 2 |
| 3 | 1984-03-01 | 25.73 | 3.247658 | 3 | 3 |
| 4 | 1984-04-01 | 25.55 | 3.240637 | 4 | 4 |
| 5 | 1984-05-01 | 29.96 | 3.399863 | 5 | 5 |
| 6 | 1984-06-01 | 31.94 | 3.463859 | 6 | 6 |
| trend | y |
|---|---|
| <int> | <fct> |
| 87 | 1 |
| 88 | 2 |
| 89 | 3 |
| 90 | 4 |
| 91 | 5 |
| 92 | 6 |
| 93 | 7 |
| 94 | 8 |
| 95 | 9 |
| 96 | 10 |
| 97 | 11 |
| 98 | 12 |
마지막 관측값으로 부터 \(Z_{n+l}(n = 30, l = 1, 2, . . . , 12)\)에 대한 95% 예측구간을 구하여라
predict_result <- as.data.frame(predict(reg, newdata = new_data, interval = "predict"))
predict_result| fit | lwr | upr | |
|---|---|---|---|
| <dbl> | <dbl> | <dbl> | |
| 1 | 4.093234 | 3.843683 | 4.342785 |
| 2 | 4.147873 | 3.898322 | 4.397424 |
| 3 | 4.324004 | 4.071398 | 4.576609 |
| 4 | 4.295602 | 4.042996 | 4.548207 |
| 5 | 4.355136 | 4.102531 | 4.607742 |
| 6 | 4.432057 | 4.179452 | 4.684663 |
| 7 | 4.371235 | 4.118629 | 4.623840 |
| 8 | 4.346016 | 4.093411 | 4.598622 |
| 9 | 4.427300 | 4.174695 | 4.679906 |
| 10 | 4.422386 | 4.169780 | 4.674991 |
| 11 | 4.464598 | 4.211992 | 4.717203 |
| 12 | 4.578264 | 4.325658 | 4.830869 |
predict_result$fitted_dep <- exp(predict_result$fit)
predict_result$fitted_dep_l <- exp(predict_result$lwr)
predict_result$fitted_dep_u <- exp(predict_result$upr)
predict_result| fit | lwr | upr | fitted_dep | fitted_dep_l | fitted_dep_u | |
|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 1 | 4.093234 | 3.843683 | 4.342785 | 59.93342 | 46.69716 | 76.92150 |
| 2 | 4.147873 | 3.898322 | 4.397424 | 63.29921 | 49.31961 | 81.24131 |
| 3 | 4.324004 | 4.071398 | 4.576609 | 75.49026 | 58.63889 | 97.18429 |
| 4 | 4.295602 | 4.042996 | 4.548207 | 73.37635 | 56.99686 | 94.46290 |
| 5 | 4.355136 | 4.102531 | 4.607742 | 77.87743 | 60.49319 | 100.25748 |
| 6 | 4.432057 | 4.179452 | 4.684663 | 84.10425 | 65.33002 | 108.27373 |
| 7 | 4.371235 | 4.118629 | 4.623840 | 79.14128 | 61.47491 | 101.88453 |
| 8 | 4.346016 | 4.093411 | 4.598622 | 77.17044 | 59.94401 | 99.34731 |
| 9 | 4.427300 | 4.174695 | 4.679906 | 83.70513 | 65.02000 | 107.75992 |
| 10 | 4.422386 | 4.169780 | 4.674991 | 83.29479 | 64.70125 | 107.23164 |
| 11 | 4.464598 | 4.211992 | 4.717203 | 86.88607 | 67.49086 | 111.85497 |
| 12 | 4.578264 | 4.325658 | 4.830869 | 97.34524 | 75.61528 | 125.31986 |
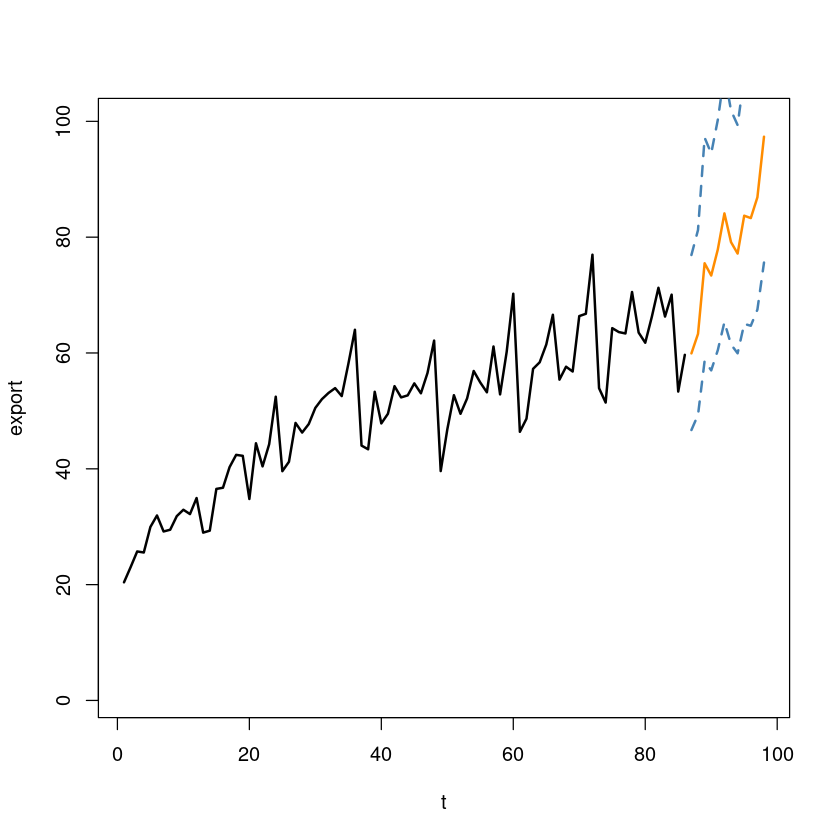
예측값 및 예측구간의 하한값과 상한값을 관측값 \(Z_t\)의 시계열과 함께 표시하여라.
plot(export~tmp.data$trend, tmp.data,
xlab = "t", ylab = "export",
xlim=c(1,98),
ylim=c(1,100),
type='l',
lwd=2)
lines(87:98, predict_result$fitted_dep, col='darkorange', lwd=2)
lines(87:98, predict_result$fitted_dep_l, col='steelblue', lwd=2, lty=2)
lines(87:98, predict_result$fitted_dep_u, col='steelblue', lwd=2, lty=2)